In my blog post for Illustrative Mathematics, Using the 5 Practices with Instructional Routines, I had the opportunity share how I am modeling the use of the 5 Practices Structure with instructional routines for teachers. If you missed this blog post, you can check it out here.
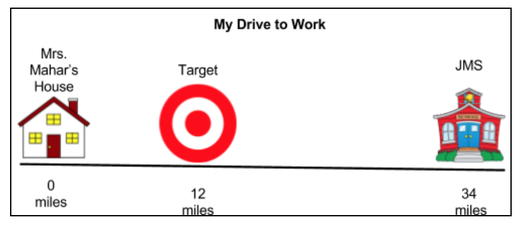
I have used this Noticing and Wondering routine to help other teachers apply the 5 Practices approach in order to help their students take ownership of their learning and clarify misconceptions. A third grade teacher was finding that her students were having difficulty solving distance problems such as the one below.
We decided to try a Notice and Wonder routine. We posted the following image on the board and recorded the noticings and wonderings in a similar manner as was done for Kiran’s box. (see blog for Illustrative Math)
The teacher could not believe that the students were solving their own distance problems during their noticings without being prompted to do so. Students that would have been previously stumped when asked what the distance between Target and JMS were when presented in a word problem were suddenly coming up with the information on their own. What attributed to the success? The activity was engaging; it was relevant to them because it was about their beloved teacher who they know loves to shop at Target and involved the school they go to. All students had an entry point, and they constructed their own meaning. After having a simple yet purposeful, successful experience in place as a foundation, the teacher reported that her students that had previously struggled with distance problems were no longer having difficulties.
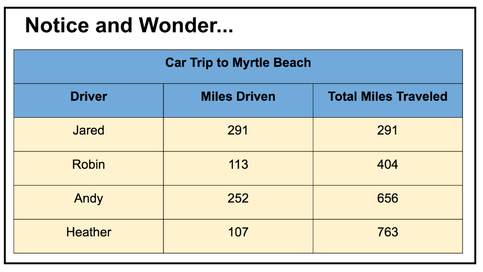
The same teacher invited me back to help her create a lesson that focused on strengthening her students ability to model their mathematical thinking through the use of representations during the problem solving process. Her students were still in the process of working on distance problems, and although they were having success with the concept, most of them were having difficulty communicating their problem solving process in a clear and concise way. A few students were using number lines to model their thinking, but the majority of students were just showing their thinking through a series of equations. I suggested we introduce the use of a table; however, we were not going to directly teach that this was a representation for communicating thinking when problem solving. I modeled a Notice and Wonder instructional routine by posting the following image on the board:
The same teacher invited me back to help her create a lesson that focused on strengthening her students ability to model their mathematical thinking through the use of representations during the problem solving process. Her students were still in the process of working on distance problems, and although they were having success with the concept, most of them were having difficulty communicating their problem solving process in a clear and concise way. A few students were using number lines to model their thinking, but the majority of students were just showing their thinking through a series of equations. I suggested we introduce the use of a table; however, we were not going to directly teach that this was a representation for communicating thinking when problem solving. I modeled a Notice and Wonder instructional routine by posting the following image on the board:
I told students that I went to on a vacation this past summer with my husband and some friends and had collected some data from our trip. I asked them what they noticed and wondered. In my planning, I had anticipated things that they would notice such as the boys drove more than the girls, and that the numbers in the column for the total miles traveled increased as you went down. I also wanted to make sure that my students noticed certain elements of the table such as the title and the headings. As students were sharing their noticings with partners, I was monitoring their conversations listening for students who noticed the key things that I wanted to highlight. I heard a student mention, that he knew I went to Myrtle Beach. I asked him how he knew, and he mentioned that the table said it. I asked him if knew what that part of the table was called, and he knew it was the title. I asked if he would share his noticing with the group. I found another student, who was discussing the miles driven and the total miles driven. I asked how she knew which numbers where which and she explained how they were organized into different columns. I asked her to if she would share that noticing with the class. When she shared her noticing with the class, we discussed what we could call the labels given on the table columns and introduced the vocabulary word of headings. The students helped introduce the format and vocabulary of the table in an authentic and relevant manner. Many mathematical noticings were uncovered in our noticings too. We wrapped up our discussion identifying how a table is one was type of representation that mathematicians use. Students then went on to work on a problem solving task that was a distance problem. Students were not instructed on how to represent their thinking. About 75% of the students used some type of a table to represent their thinking when solving their distance problem. The teacher was amazed at how an instructional routine can be an impactful vehicle for helping students to begin to unpack their learning. She continues to apply these types of instructional routines with the 5 Practices Structure, so that the her students can own their learning.
I would love to hear about your experiences with implementing the 5 Practices with an instructional routine such as Notice and Wonder.


 RSS Feed
RSS Feed
